std::accumulate

Part 0

The Most Powerful Algorithm in the World?

A Long Time Ago, In a Galaxy etc…

Part 1

Accumulatable Things

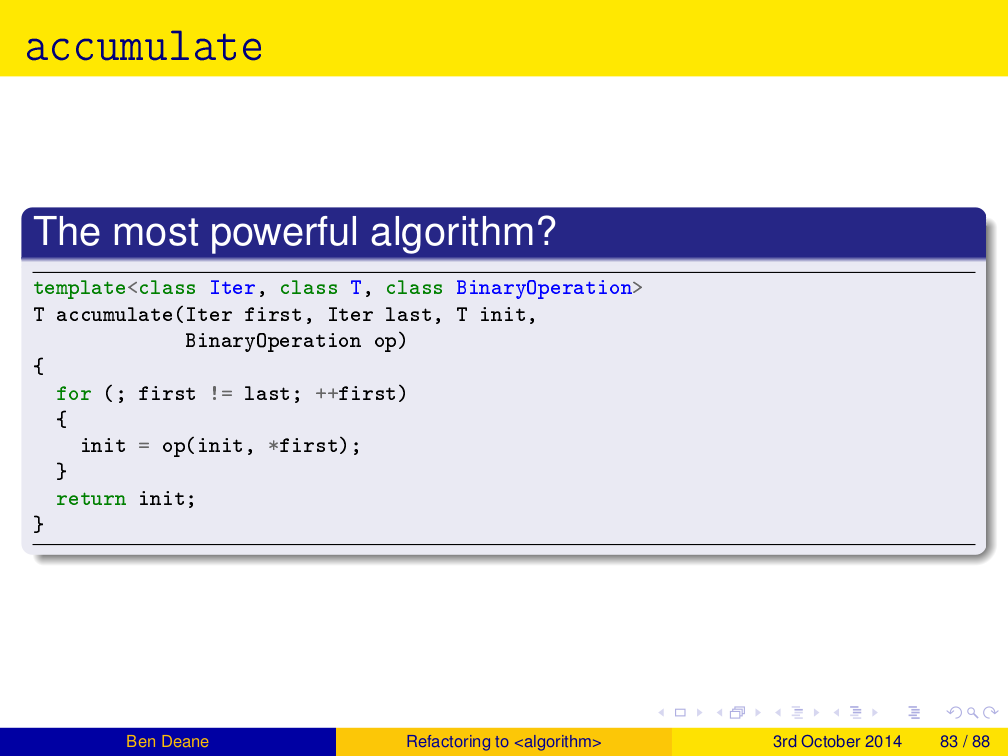
std::accumulate

template <class InputIt, class T, class BinaryOp>
T accumulate(InputIt first, InputIt last,
             T init, BinaryOp op)
{
  for (; first != last; ++first) {
    init = op(init, *first);
  }
  return init;
}

Typical uses

vector<int> v = {1,2,3,4,5};

int sum = accumulate(v.cbegin(), v.cend(), 0, plus<>{});
cout << sum << '\n';

int product = accumulate(v.cbegin(), v.cend(), 1, multiplies<>{});
cout << product << '\n';

Of course, this is not why you're here. What else can we accumulate?

How about finding a min or max?

vector<unsigned> v = {1,2,3,4,5};

unsigned max_val = accumulate(v.cbegin(), v.cend(), 0,
    [] (unsigned a, unsigned b) { return a > b ? a : b; });
cout << max_val << '\n';

How about finding a min or max?

Value-based min_element or max_element

template <typename It, typename Compare,
          typename T = typename iterator_traits<It>::value_type>
T min_element(It first, It last, Compare cmp)
{
  // precondition: first != last
  auto init = *first;
  return accumulate(
      ++first, last, init,
      [&] (const T& a, const T& b) {
        return cmp(b, a) ? b : a;
      });
}

What about bool values?

bool results[] = {true, false, true, true, false};

bool all_true = accumulate(cbegin(results), cend(results),
                           true, logical_and<>{});
bool some_true = accumulate(cbegin(results), cend(results),
                            false, logical_or<>{});
bool none_true = !accumulate(cbegin(results), cend(results),
                             false, logical_or<>{});

Not that interesting yet…

The signature of the function

Type1 fun(const Type1 &a, const Type2 &b);

So far, we've looked at Type1 and Type2 being the same.

Things get more interesting when they differ.

A more interesting bool case

map<int, weak_ptr<thing>> cache;

shared_ptr<thing> get_thing(int id) {
  auto sp = cache[id].lock();
  if (!sp) make_async_request(id);
  return sp;
}

void load_things(const vector<int>& ids)
{
  bool all_cached = accumulate(
    ids.cbegin(), ids.cend(), true,
    [] (bool cached, int id) {
      return get_thing(id) && cached;
    });
  if (!all_cached)
    service_async_requests();
}

bool As the Result

We use many function results as boolean values in control flow.

• actual bool
• pointers
• zero-result of a comparison trichotomy
• anywhere else we want to write if (x)

This means we can use accumulate to collect these function values. (Similar to all_of, any_of, none_of, but where we don't want the short-circuiting behavior.)

More things…

• joining strings
• building requests from key-value pairs
• merging JSON objects
• multiplying matrices

What do all of these have in common?

You All Remember Monoids?

A set of objects and an operation such that:

• The operation is closed over the set
• The operation is associative
• There is an identity element

Building HTTP headers: Before

curl_slist* curl_headers = NULL;
for (auto it = headers.begin();
     it != headers.end(); ++it)
{
  curl_headers = curl_slist_append(curl_headers,
    (format("%s: %s") % it->first % it->second).str().c_str());
}

Building HTTP headers: After

curl_slist* curl_headers = accumulate(
    headers.cbegin(), headers.cend(), static_cast<curl_slist*>(nullptr),
    [] (curl_slist* h, const auto& p) {
        return curl_slist_append(h,
          (format("%s: %s") % p.first % p.second).str().c_str());
      });

Monoids Are Everywhere!

Monoids are everywhere, and any monoid can be accumulated:

• addition on integers
• concatenation on strings
• union on sets
• "merging" objects of all kinds
• max, min, and, or, …
• parsing
• many more things…

More Monoid Observations

A type may be a monoid in more than one way (under more than one operation).

A function that returns a monoid is a monoid.

An aggregate of monoids is a monoid. (e.g. map<K,V> where V is a monoid)

Why not just write a loop?

Some advantages to accumulate

• No declaration/initialization split
• It's often easier to write a binary function
  • Or a unary function with monoidal output
  • Simplifies an API
• Incremental computation
  • Can accumulate by parts
• Potential for parallel computation

What accumulate Can Do

• Turn binary functions into n-ary functions
• Collect results of functions whose outputs are monoidal
• Allow part-whole hierarchies to be treated uniformly
  • which unlocks parallel computation

Part 2

Aside: Parallel Computations and Monoids

Distributed Accumulate

Distributed Accumulate

std::reduce

template <class InputIt, class T, class BinaryOp>
T reduce(InputIt first, InputIt last,
         T init, BinaryOp op);

The same as accumulate, except the sequence may be processed in any order (and perhaps in parallel according to policy).

This works because of associativity (semigroup property).

We lose the type variation, but gain parallelism.

Big Data Monoids Everywhere

• averages (regular or decayed)
• top-N calculations
• histograms
• bloom filters
• Gaussian distributions
• count-min sketch
• Hyperloglog

HyperLogLog

From http://content.research.neustar.biz/blog/hll.html

Algebraic Structures in Big Data

• monoids and semigroups are the key to parallelism
• the ability to combine "summary data"
• expensive training happens once

Part 3

Nonlinear Structures

accumulate Works on Linear Sequences

How would we make it work on multi-dimensional structures?

Maybe we can define a linear traversal on the structure (in-order, pre-order, post-order)…

But the nodes are still homogeneous…

What if it's a bit more complex? (Like say, a JSON object?)

Recall std::accumulate

template <class InputIt, class T, class BinaryOp>
T accumulate(InputIt first, InputIt last,
             T init, BinaryOp op);

The T here deals with an empty sequence.

The BinaryOp deals with a non-empty sequence.

Recursive Definition of a vector

We can view "sequence accumulation" as handling two cases:

• an empty vector
• a vector consisting of an element plus another vector

This is the sort of recursive definition we find in functional languages. And it's the key to accumulating other data structures.

std::accumulate Viewed Recursively

template <typename It, typename EmptyOp, typename NonEmptyOp>
auto recursive_accumulate(It first, It last,
                          EmptyOp op1, NonEmptyOp op2)
{
  if (first == last) return op1();
  --last;
  return op2(recursive_accumulate(first, last, op1, op2), *last);
}

T (here EmptyOp) is really a function from empty vector to T

BinaryOp (here NonEmptyOp) is really a function from (element, vector) to T

Accumulating a variant

struct JSONWrapper;
using JSONArray = vector<JSONWrapper>;
using JSONObject = map<string, JSONWrapper>;
using JSONValue = variant<bool,
                          double,
                          string,
                          nullptr_t,
                          JSONArray,
                          JSONObject>;
struct JSONWrapper
{
  JSONValue v;
  operator JSONValue&() { return v; }
  operator const JSONValue&() const { return v; }
};

Example: Render a JSONValue as a string

We need a function for each distinct type that can be inside the variant.

string render_json_value(const JSONValue& jsv);

string render_bool(bool b) { return b ? "true" : "false"; };
string render_double(double d) { return to_string(d); };
string render_string(const string& s)
{
  stringstream ss;
  ss << quoted(s);
  return ss.str();
}
string render_null(nullptr_t) { return "null"; }

Example: Render a JSONValue as a string

We need a function for each distinct type that can be inside the variant.

string render_array(const JSONArray& a)
{
  return string{"["}
    + join(a.cbegin(), a.cend(), string{","},
           [] (const JSONValue& jsv) {
             return render_json_value(jsv);
           })
    + "]";
}

Example: Render a JSONValue as a string

We need a function for each distinct type that can be inside the variant.

string render_object(const JSONObject& o)
{
  return string{"{"}
    + join(o.cbegin(), o.cend(), string{","},
           [] (const JSONObject::value_type& jsv) {
             return render_string(jsv.first) + ":"
               + render_json_value(jsv.second);
           })
    + "}";
}

Example: Render a JSONValue as a string

We need a function for each distinct type that can be inside the variant.

string render_json_value(const JSONValue& jsv)
{
  return fold(jsv,
              render_bool, render_double, render_string,
              render_null, render_array, render_object);
}

A Generic fold for variant

template <typename... Ts, typename... Fs>
auto fold(const variant<Ts...>& v, Fs&&... fs)
{
  static_assert(sizeof...(Ts) == sizeof...(Fs),
                "Not enough functions provided to variant fold");
  return fold_at(
      v, v.index(),
      forward<Fs>(fs)...);
}

A variant, and N functions (one for each case of the variant).

Recall that the "zero value" is implicit in the functions if required.

A Generic fold for variant

template <typename T, typename F, typename... Fs>
static auto fold_at(T&& t, size_t n, F&& f, Fs&&... fs)
{
  using R = decltype(f(get<0>(t)));
  return apply_at<0, sizeof...(Fs)+1>::template apply<R, T, F, Fs...>(
      forward<T>(t),
      n,
      forward<F>(f),
      forward<Fs>(fs)...);
}

A Generic fold for variant

template <size_t N, size_t Max>
struct apply_at
{
  template <typename R, typename T, typename F, typename... Fs>
  static auto apply(T&& t, size_t n, F&& f, Fs&&... fs)
  {
    if (n == N)
      return forward<F>(f)(get<N>(forward<T>(t)));
    else
      return apply_at<N+1, Max>::template apply<R, T, Fs...>(
          forward<T>(t),
          n,
          forward<Fs>(fs)...);
  }
};

A Generic fold for variant

template <size_t Max>
struct apply_at<Max, Max>
{
  template <typename R, typename T, typename... Fs>
  static auto apply(T, size_t, Fs...)
  {
    assert("Variant index out of range" && false);
    return R{};
  }
};

Generic variant accumulation

template <typename... Ts, typename... Fs>
auto fold(const variant<Ts...>& v, Fs&&... fs)

Hmm, this looks a lot like visitation.

Recursive reduction

Any recursively-specified data structure can be accumulated using "visitation" to produce a monoidal value which is accumulated.

• tree -> string rendering
• depth, fringe of trees
• lighting contributions
• scene graph operations
• etc, etc

This is a useful alternative when dealing with heterogeneous hierarchies that it is difficult to define a linear traversal for.

Part 4

Heterogeneous Sequences

Beyond Monoids

template <class InputIt, class T, class BinaryOp>
T accumulate(InputIt first, InputIt last,
             T init, BinaryOp op);

Type1 fun(const Type1 &a, const Type2 &b);

Type1 and Type2 can be different: this is saying that we know how to "fold" values of Type2 into values of Type1.

Heterogeneous Folding

template <typename T>
Accumulator fun(const Accumulator &a, const T &b);

What if T varied all the time? We could have cases where we know how to "fold" lots of different types into an accumulated value.

The Obvious Example

template <typename T>
ostream& operator<<(ostream& s, const T &t);

The Obvious Example

auto t = make_tuple("Hello", 3.14, 1729, 'a');
auto f = [] (ostream& s, const auto& x) -> ostream& {
  return s << x << '\n';
};
fold(t, cout, f) << "done" << endl;

$ ./a.out
Hello
3.14
1729
a
done
$

Heterogeneous Folding

template <typename F, typename Z, typename... Ts>
decltype(auto) fold(const tuple<Ts...>& t, Z&& z, F&& f);

(Implementation left as an exercise - link at the end)

Different Types of Accumulation

• accumulate
  • 1 function, linear homogeneous structure
• accumulate with linear tree traversal
  • 1 function, multidimensional homogeneous structure
• variant-fold
  • n functions, multidimensional heterogeneous structure
• tuple-fold
  • n functions, linear heterogeneous structure

The empire so far… all of these could also be parallel, given the appropriate monoidal (or semigroup) structure.

Part 5

The Opposite of Accumulate?

Fold? Unfold

If accumulate is folding up a data structure to produce a value…

The opposite is "unfolding" a seed value to produce a data structure.

How To Unfold

template <typename InputIt, typename T, typename F>
T accumulate(InputIt first, InputIt last, T init, F f);

template <typename OutputIt, typename T, typename F>
OutputIt unfold(F f, OutputIt it, T init);

F will be repeatedly called with a "reducing" T value and write the result(s) to the output it.

• What should the signature of F be?
• How do we know when we're done?

Signature of the Function Passed to unfold

F is the opposite of accumulate's BinaryOp

Type1 fun(const Type1 &a, const Type2 &b);

It's clear that F needs to return a pair

• result (say of type U) to write into the output range
• new value of T to feed into next invocation of F

In general the "result to write to the iterator" may be a range or sequence of values.

Three Choices for unfold Termination

// 1. provide a sentinel value of type T
template <typename OutputIt, typename T, typename F>
OutputIt unfold(F f, OutputIt it, T init, T term);

Choice 1: terminate when a termination value (of type T) is returned.

Three Choices for unfold Termination

// 2. provide a sentinel value of type (other thing returned by F)
template <typename OutputIt, typename T, typename F, typename U>
OutputIt unfold(F f, OutputIt it, T init, U term);

Choice 2: terminate when a termination value (of type U) is returned.

Three Choices for unfold Termination

// 3. F will return an optional
template <typename OutputIt, typename T, typename F>
OutputIt unfold(F f, OutputIt it, T init);

Choice 3: F returns an optional; terminate when nullopt is returned.

How To Unfold

template <typename OutputIt, typename T, typename F>
OutputIt unfold(F f, OutputIt it, T&& init)
{
  for (auto o = f(forward<T>(init)); o;
       o = f(move(o->second))) {
    it = move(begin(o->first), end(o->first), it);
  }
  return it;
}

F returns optional<pair<range, T>>

Unfold Example

 1: optional<pair<string, int>> to_roman(int n)
 2: {
 3:   if (n >= 1000) return {{ "M", n-1000 }};
 4:   if (n >= 900) return {{ "CM", n-900 }};
 5:   if (n >= 500) return {{ "D", n-500 }};
 6:   if (n >= 400) return {{ "CD", n-400 }};
 7:   if (n >= 100) return {{ "C", n-100 }};
 8:   if (n >= 90) return {{ "XC", n-90 }};
 9:   if (n >= 50) return {{ "L", n-50 }};
10:   if (n >= 40) return {{ "XL", n-40 }};
11:   if (n >= 10) return {{ "X", n-10 }};
12:   if (n >= 9) return {{ "IX", n-9 }};
13:   if (n >= 5) return {{ "V", n-5 }};
14:   if (n >= 4) return {{ "IV", n-4 }};
15:   if (n >= 1) return {{ "I", n-1 }};
16:   return nullopt;
17: }

Unfold Example

int main()
{
  string r;
  unfold(to_roman, back_inserter(r), 1729);
  cout << r << '\n';
}

$ ./a.out
MDCCXXIX
$

Fold and Unfold are Really the Same

Just transformations on a data structure.

Which you use is a matter of convenience.

We think of accumulate as working on structures and producing values, and unfold vice versa.

But structures are themselves values…

Postscript

The Fruits of Algorithmic Perversions

The Question

If you were stuck on a desert island, which algorithms would you take with you?

Maybe some "building block" algorithms?

• partition
• rotate
• reverse

Maybe some others?

Which algorithms are the most powerful?

What if you couldn't write any loops, so you're stuck with what you have?

The Algorithms (pre-C++17)

Of 90 total, 77 are basically "plain loops"

Why Doesn't accumulate Work on Iterators?

template <class InputIt, class T, class BinaryOp>
T accumulate(InputIt first, InputIt last,
             T init, BinaryOp op)
{
  for (; first != last; ++first) {
    init = op(init, *first);
  }
  return init;
}

The function receives a value rather than an iterator…

Why Doesn't accumulate Work on Iterators?

template <class InputIt, class T, class BinaryOp>
T accumulate(InputIt first, InputIt last,
             T init, BinaryOp op)
{
  for (; first != last; ++first) {
    init = op(init, first);
  }
  return init;
}

With this formulation, we can view an iterator as an accumulator value.

Abusing accumulate

I'm the first to admit that some of these algorithm implementations are… interesting.

• find (using exceptions for control flow)
• reverse (using forward iterators and a function as the accumulator)

But…

Some interesting alternatives arise.

• find_if -> find_all?
• adjacent_find -> adjacent_find_all?
• min_element that returns an optional value?
• sort with forward iterators?

Hunting for (Raw?) Loops, Redux

Almost everything can be expressed as some form of accumulation.

Should it be? That's for you to decide.

But when you get used to seeing monoids, everything is monoids.

Some Further Reading

• Fold (Haskell Wiki)
• An Introduction to Recursion Schemes
• Gaussian Distributions form a Monoid
• Add ALL the Things: Abstract Algebra Meets Analytics
• Variant folding code
  • http://gist.github.com/elbeno/e5c333fff247e78990e08ab8ed56aecd
• Tuple folding code
  • http://gist.github.com/elbeno/95e710c04d56d8cc72ade2e6b2bbe9d5

Accumulation Power

• Any time you write an API, see if any of your data types form a monoid or a semigroup under any operations you provide.
• Look for opportunities where you are applying a function in a loop.
• Monoids are everywhere.
• Think about folding with multidimensional structures or heterogeneous sequences.
• Unfolds are an alternative way to think of things; can be combined with folds to produce arbitrary structural transformations.
• Algorithmic perversions can be fruitful in terms of learning…
• Accumulation: not just for adding things up!